[월간 코드 챌린지 시즌1] 11월 문제 해설

코딩이 재미있는 사람들을 위한 월간 코드 챌린지 시즌1이 종료되었습니다. 2020년 11월 5일에 진행된 마지막 대회 문제들에 대한 간단한 해설을 공개합니다.

 

[1번 문제] 내적

출제의도

• 주어진 로직을 구현할 수 있는지

해설

말 그대로 두 배열의 내적을 구하는 문제입니다. for문 등의 반복문을 활용하여 문제에서 주어진 로직을 구현할 수 있습니다.

시간복잡도는 $O(n)$ 입니다. ($n$은 배열의 길이)

 

[2번 문제] 이진 변환 반복하기

출제의도

• 진법 변환을 적절하게 응용할 수 있는지

해설

x의 모든 0을 제거한 후 남은 문자열의 길이는, x에 들어있는 모든 1의 개수임을 알 수 있습니다. 어떤 정수 x를 2진법 문자열로 표현하는 함수를 만들고, 지문에 주어진 로직을 그대로 따라가면 문제를 풀 수 있습니다.

시간복잡도는 $O(n)$ 입니다. ($n$은 초기 문자열의 길이) 왜냐하면 매 이진 변환마다 길이가 $x \rightarrow \log{x}$ 식으로 아주 많이 줄어들기 때문이고, 이 길이들을 다 더해봐야 $2n$ 보다 작기 때문입니다.

 

[3번 문제] 스타 수열

출제의도

• 그리디(Greedy) 알고리즘을 적절하게 활용할 수 있는지

해설

어떤 스타 수열 $x[0], x[1], \ldots, x[2n-1]$ 에 대해서, 그 스타 수열을 2개씩 끊어서 만든 집합의 공통 원소를 $c$라고 하면, $c$가 아닌 다른 값들이 들어갈 자리에는 $c$를 제외한 어떤 값이 들어가든 별로 중요하지 않습니다.

따라서, 공통 원소로 가능한 모든 $c$ 값에 대해서, 이 $c$ 값으로 만들어낼 수 있는 가장 큰 스타 수열의 길이를 찾는 방법을 생각해볼 수 있습니다.

가능한 모든 $c$ 값에 대해, 각 값의 모든 위치들을 미리 저장한 후, 다음과 같은 과정을 거치면 문제를 풀 수 있습니다.

1. $a[i] = c$인 모든 $i$를 $i_1, i_2, \ldots, i_k$ 라고 합시다.
2. 빈 수열 $x$를 만듭니다. 이 수열을 스타 수열로 만들고자 합니다.
3. $i_1, i_2, ..., i_k$에 대해서, 각 인덱스와 그 인덱스의 바로 앞 또는 바로 뒤를 스타 수열에 포함시킬 수 있다면 그 인덱스들의 값을 스타 수열에 포함시킵니다.

위 과정을 거쳐 만들어진 $x$가 빈 수열이라면 해당 $c$로는 스타 수열을 만들 수 없는 셈입니다. (실제 그런 경우는 배열 내 모든 원소가 같은 값일 때밖에 없습니다.) 그렇지 않다면, 가능한 모든 $x$ 수열 중에서 가장 긴 $x$의 길이를 골라 return 하면 됩니다.

시간복잡도는 $O(n)$ 입니다. ($n$은 초기 수열 $a$의 길이입니다.)

또한, 이 문제는 DP(Dynamic Programming)로도 해결이 가능합니다. 한번 도전해보세요!

 

[4번 문제] 가짜 해밀토니안

출제의도

• 트리 DP(Dynamic Programming on Tree)를 적절하게 활용할 수 있는지

해설

가짜 해밀토니안 경로를 가지는 트리의 특성은 다음과 같습니다.

• 메인 경로가 하나 있고, 그 경로 상에 있는 모든 노드들에 대해서, 해당 노드에서 출발하는 일자형으로 뻗은 서브 경로가 최대 1개 있는 트리

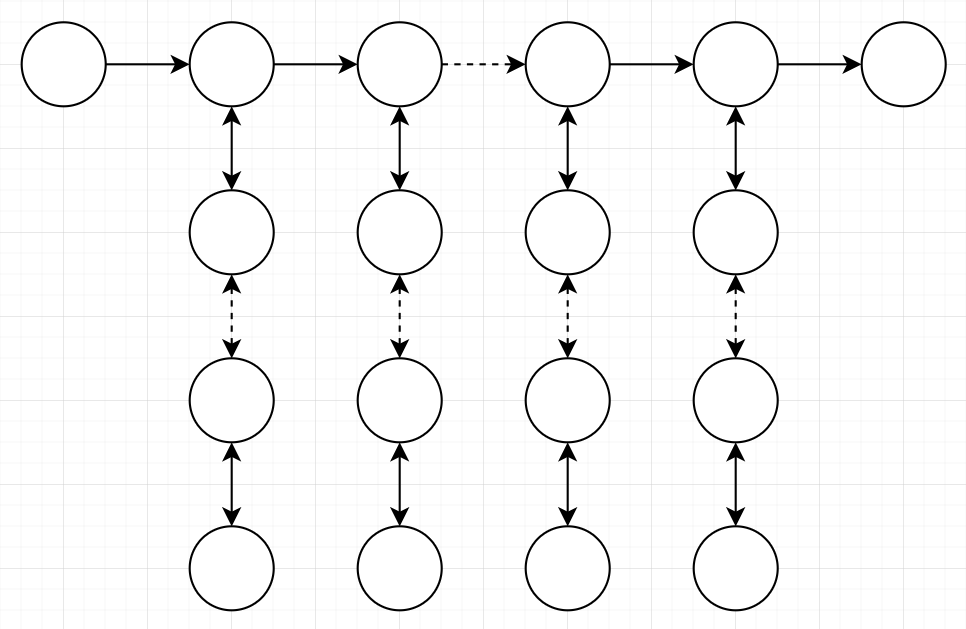
가짜 해밀토니안 경로를 가지는 트리와 그 경로의 예시입니다.

 

가짜 해밀토니안 경로를 가지는 트리의 특성이 이런 이유는 다음과 같습니다.

1. Degree가 4 이상인 점을 가지는 것이 불가능합니다. 해당 점을 최소 3번 이상 왕복해야 하기 때문입니다.
2. Degree가 3인 점의 경우, 인바운드(들어오는 경로)와 아웃바운드(나가는 경로) 이웃을 결정하면 나머지 한 이웃으로는 오직 왕복 일자형으로만 움직일 수 있습니다.

이러한 서브트리의 크기를 구하기 위해서 트리 DP를 사용합니다. DP 과정 중에 BBST(Balanced Binary Search Tree) 등의 자료구조 등을 사용하여 시간복잡도 $O(n \log n)$ 안에 풀 수 있습니다.

 

 

월간 코드 챌린지 11월 문제 다시 풀기

월간 코드 챌린지 11월 문제는 프로그래머스에서 다시 풀 수 있습니다. 여기를 클릭 후 왼쪽 하단의 '문제 모음' 필터 조건에 월간 코드 챌린지 시즌1을 선택하세요. 그럼 2021년에 시즌2로 다시 뵙겠습니다!